Basic Fractals

　

Georg Cantor (1848-1914)是一位德國理論數學家，在1883出版The Cantor Set與相關概念，The Cantor Set之所以會與碎形幾何一起被討論是關於其曖昧的特質。所謂The Cantor Set，是指一個＜0,1＞的單元距離，取出其中間的三分之一＜ 1/3＞保留兩端，當此程序無線的重複時，一個線段就成為無限的點。

　

The Cantor Set清楚了說明兩個重要的特色涉及於碎形結構與自然結構，首先是自我相似性：小尺度的比例相似於大尺度的比例，這自我相似性也存在於自然結構中，但自然的自我相似性並沒有延伸至無限並且包含一些隨機的變化，第二個特色是The Cantor Set中聚集成群的點，自然系統中，從夜晚的星空至花椰菜的外型，展現一種聚集成群的布置，而不是平坦的。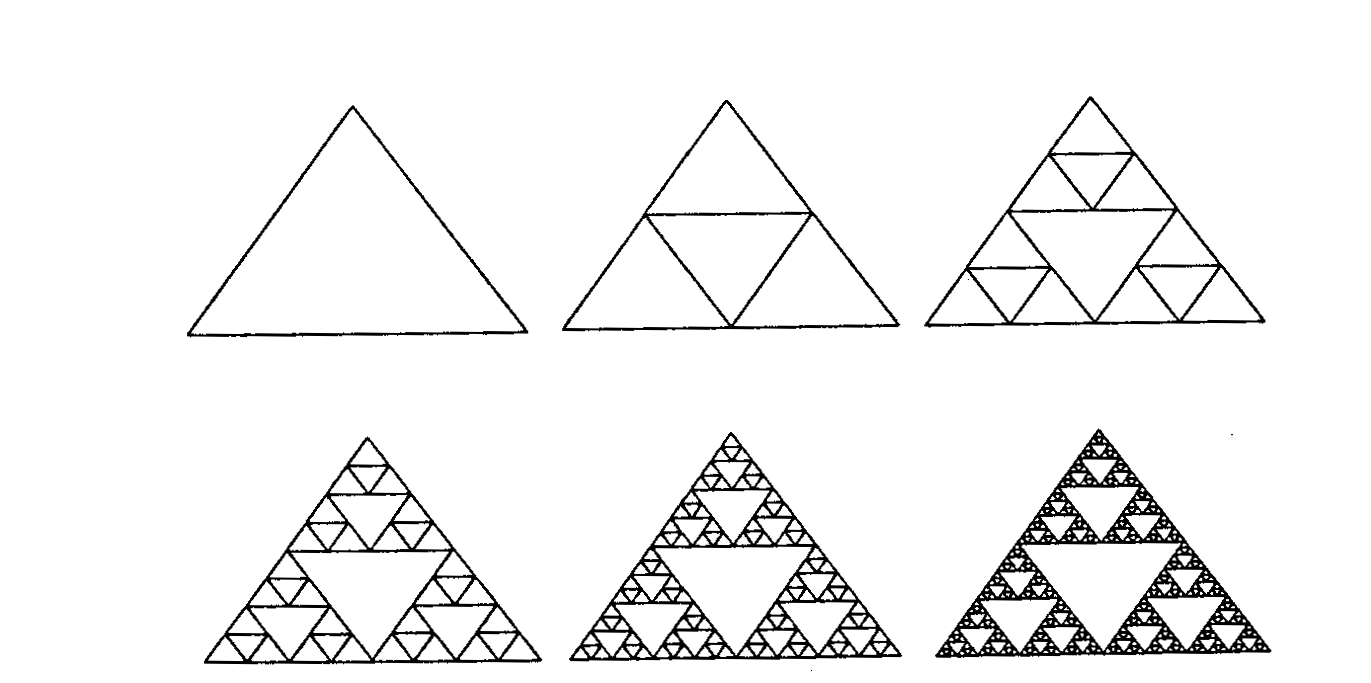

相同的例子在1919年，波蘭數學家Waclaw Sierpinski (1882-1969)發表一篇論證＜The Slerpinsld Gasket＞，說明一個等腰三角形，取出中間的一相似部分，在多次重複後是相同的道理。

　

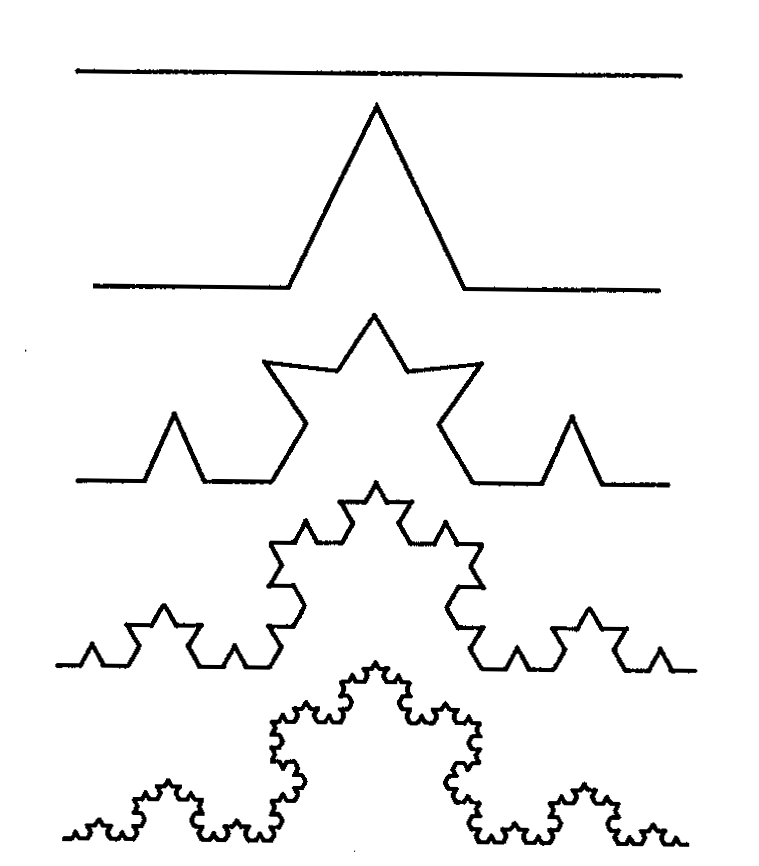
瑞典數學家Helge van Koch在1904年，構想出如何測量建構連續弧線的方法＜The Koch Curve＞，The Koch Curve原本是一條筆直的線段，分成三部分，取出中間的一段後，在中間的部分放回等邊三角形，當此程序一直不斷被重複後，一段筆直的線就成為一連續的弧線，當弧線一直在不斷重複後，也就代表著是無限長，筆直的線已不存在最後的弧線中。這中間加入的等邊三角形線段是一個關鍵性的因素，這是一個重要的概念，碎形幾何之所以存在真實的數學現象中是由其不斷的繁衍（generation），這是一個純粹的數學想法，迄至這些理論家，還沒發展到設計領域的概念上。

　

　

  • The Minkowski Curve

  • The Peano Curve

    • 　

    在這些眾多弧線理論之後，可以窺見一種趨勢，碎形的觀念可以將幾何從一度空間、推及到二度空間，甚至三度空間的可能。在二度空間上（編織物）已存有想像的可能，但如何應用至三度空間，最好的例子就是：血液在人類身體的分佈狀況，血液在身體的分佈狀況類似於一個三度空間的樹狀結構，是一個Space-Filling Curves.

    　

    在＜A History of Architecture＞（Banister Fletcher）書中，說明建築物與建築物的組成，複雜的外型與大小尺度的凹凸。例如：希臘與羅馬平面配置的細部，其結果就樣隨意的畫許多Koch Curve在描圖紙上，任意的堆疊的結果。就建築外型的的操作中，碎形幾何串連（cascade）的觀念，可以發展至設計中，例如：Perter Eisenman在法蘭克福大學中生物研究中心的一個設計案。

    　

    在＜Fractals＞（Hans Lauwerier）此書中，說明數字系統與碎形之間的關係，例如：the Cantor set是涉及一個三段數字系統的關係。此關係可以運用在電腦的編碼中。